Inscribed Angle Theorem of Thales

The original theorem, as stated by the Greek mathematician Thales, is all triangles inscribed in a circle with two corners diametrically opposed are right triangles. Note: right triangles are triangles with one angle that is 90 degrees (a right angle).

Lesson

First look at some of the example triangles inscribed in the circles below. They all appear to be right triangles.

Proof

Although all the examples drawn above have right angles (the angles with yellow square), that doesn’t prove that all such inscribed triangles should be right triangles.

The proof of Thales uses three known facts that were previously established by early mathematicians. Fact 1 is that all points on a circle are the same distance from the center of the circle (this is actually the definition of a circle). Fact 2 is that any triangle with two equal sides (an isosceles triangle) also has two equal angles. Fact 3 is that the sum of the interior angles of a triangle equals 180 degrees (this is also another lesson in this book). Let’s draw an inscribed triangle within the circle and we’ll label the angles of the triangle as A, B, C.

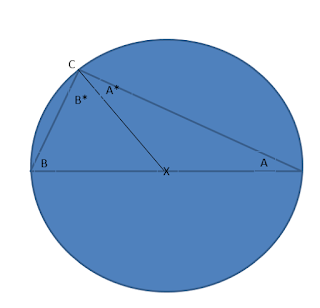
For the next step of the proof, we’ll add a new point, X, on the diameter at the center of the circle. Draw a line from X to the corner at angle C (shown above).  Also, the angle C is now split into two angles which are labelled A* and B*. 

We’ll use the three given facts from above. Using Fact 1, the length of line XC equals the length of line XA. Using Fact 2, the triangle AXC has two sides of equal length therefore the angle A* is the same as the angle A.

Repeating these steps for the BXC; using Fact 1 the lengths of lines XB and XC are the same. Using Fact 2, angle B* is the same as angle B.

Finally using Fact 3, the angles A + B + C = 180 degrees. Angle C equals A* + B* which is the same as A+B.  Substituting C for A+B in Fact 3 gives us C + C = 180 degrees or 2C= 180 degrees. Therefore angle C = 180/2 = 90 degrees (or angle C is a right angle).

Alternate Application

The theorem can also be used in reverse to locate the center of any circle. Start with any circle and place a sheet of rectangular paper (any size will do) so a corner is touching the circle (see point A). Mark the points where the two sides coming off that corner intersect the circle (see points B and C). Draw a line between points B and C – these points are now diametrically opposed.

Update 8/23/2021:

Some believe Thales should be given credit for first visualizing a proof to the Pythagorean Theorem: See: Should we rename the Pythagorean theorem? - Big Think.