(Image: Gemini created)
Instructions
Begin with any number (limited to positive integers: 1, 2, 3, 4…). Follow
these two simple rules to obtain the next number in the sequence:
Rule 1: If the number is
even, divide it by 2
or
Rule 2: If the number is
odd, triple it and add 1
If this next number is 1, stop;
that is the end of the sequence. For any number other than one, use Rules 1 and
2 above to obtain the next number in the sequence. Continue using the rules and
build up the sequence until you end at the number 1. The name “HOTPO” is based
on the initials of the rules “Half Or Triple
Plus One.”
Example 1
Starting number: 4
Since 4 is even, divide by two.
The next number in the sequence is 2.
Since 2 is even, divide by two.
The next number in the sequence is 1.
We reached 1 so now the sequence
ends. The full sequence was: 4, 2, 1.
Example 2
Starting number: 3
Since 3 is odd, triple it and add
one. The next number in the sequence is 3 x 3 + 1 = 10.
Since 10 is even, divide by two.
The next number in the sequence is 5.
Since 5 is odd, triple it and add
one. The next number in the sequence is 3 x 5 + 1 = 16.
Since 16 is even, divide it by
two. The next number is 8.
Since 8 is even, divide it by
two. The next number is 4.
Since 4 is even, divide it by
two. The next number is 2.
Since 4 is even, divide it by
two. The sequence now ends with 1.
The full sequence was 3, 10, 5, 16, 8, 4, 2, 1.
The two examples above show how
the HOTPO sequence can develop and grow. Sometimes the sequence ends very
quickly and other times the sequence goes up and down but eventually settles to
1. The interesting thing is that no matter what number you start with, the
sequence will end with 1.
Suggested Exercises
1.
Find the starting number
under 10 that produces the longest sequence.
2.
Find the starting number
under 10 that produces the shortest sequence.
3.
Find the starting numbers
between 20 and 100 that produce the shortest and longest sequences.
4.
Compete with a friend,
classmate or family member to find the starting number with the longest
sequence.
Sequences made by other rules
The HOTPO rules always produce
sequences that end in 1. This is not the case for sequences produced by other
rules. Explore the sequences that are created by a different set of rules
described below.
Start with any positive integer.
To obtain the next number in the sequence:
Rule 1:
If the number is even, divide by 2 (same rule as before)
Or
Rule 2:
If the number is odd, triple it and add 3
If the new number is 1, stop;
otherwise continue.
Examples:
Starting number: 2
The number is even, so divide by
two. The next number is 1 so the sequence ends. The full sequence is simply 2,
1.
Starting number: 3
The number is odd, so triple and
add 3. The next number is 3 x 3 + 3 = 12.
The number is even, so divide by
2. The next number is 6.
The number is even, so divide by
2. The next number is 3.
The number is odd, so triple and
add 3. The next number is 3 x 3 + 3 = 12.
The number is even, so divide by
2. The next number is 6.
The number is even, so divide by
2. The next number is 3.
The sequence is now stuck in a
cyclic loop. The full sequence is: 3, 12, 6, 3, 12, 6, 3, 12, 6, 3…
Exercises
5.
Try this “Half or Triple
plus Three” sequence for other starting numbers up to 11. What results do you
see?
6.
Explore other sequences by
making your own rules.
7.
(For advanced students):
Try the original HOTPO rules applied to negative numbers.
For parents, teachers and advanced thinkers - How does it
work?
This lesson is based on the
Collatz Conjecture which states that the HOTPO sequence will always end in 1
for all starting numbers that are positive integers. A conjecture is a
mathematical statement that is generally accepted as true but has not been
proven. A formally proven statement is called a theorem. While the Collatz
Conjecture has not been proven, it has been confirmed to be true using
computers for integers beyond 1,000,000,000. Monetary prizes are available for
the person who can formally prove the Collatz statement to be true. If a single
starting number was found for which the HOTPO sequence does not end with 1, then
the Collatz statement would be disproven. However, given the very large numbers
that have already been tested, finding such a starting number is unlikely.
For additional information:
Exercise key and comments:
1.
The length of the HOTPO
sequence starting with 9 is 20 numbers in length:
9, 28, 14, 7, 22, 11, 24, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
2.
The shortest sequence
starts with 2 with just 2 numbers in length: 2, 1. (One might also consider the
case of the starting number of 1 if you say you reached one before applying
Rule 1 or 2; however, following the rules you would first triple one and add
one to get a second number of 4 so the sequence should be: 1, 4, 2, 1 for a
total of numbers in the sequence.)
3.
The shortest sequence for
starting numbers 20 to 100 begins with 32: 32, 16, 8, 4, 2, 1.
The longest sequence for starting numbers 20 to 100 begins with 97 (it takes
118 steps to complete).
4.
Suggestions for competing
with a friend or classmate:
a. find longest sequence with a time limit of 30 minutes (or other time of your
choosing)
b. compete once without the use of calculators and once using calculators.
5.
The rule Half or Triple
Plus Three produces the following sequences for the starting numbers of 1-11:
Starting Number: Sequence:
1
1, 6, 3, 12, 6, 3, 12, 6,
3 …
2
2, 1
3
3, 12, 6, 3, 12, 6, 3…
4
4, 2, 1
5
5, 18, 9, 30, 15, 48, 24,
12, 6, 3, 12, 6, 3…
6
6, 3, 12, 6, 3…
7
7, 24, 12, 6, 3, 12, 6, 3…
8
8, 4, 2, 1
9
9, 30, 15, 48, 24, 12, 6,
3, 12, 6, 3…
10
10, 5, 18, 9, 30, 15, 48,
24, 12, 6, 3, 12, 6, 3…
11
11, 36, 18, 9, 30, 15, 48,
24, 12, 6, 3, 12, 6, 3…
12
12, 6, 3, 12…
13
13, 42, 21, 66, 33, 102,
51, 154 (and continues 23 more terms before cycling back to 33, 102, 51…)
6.
Suggestions for your own
rules for creating sequences:
a. Keep to two rules based on the seed number (if even do this; if odd do that)
b. Explore the sequences created by your rules with larger and larger starting
numbers until you see that the sequences end in cycles or the sequence of
numbers gets larger without end.
c. Suggestions: Try Half or Triple Minus One (some starting numbers will
terminate with one and some end in a cyclic loop).
7.
(Advanced) Applying the
HOTPO rules to negative numbers produces cyclic results:
Starting Number: Sequence:
-1 -1,
-2, -1 …
-2 -2,
-1, -2, -1 …
-3 -3, -8,
-4, -2, -1, -2, -1 …
-4 -4,
-2, -1, -2, -1 …
-5 -5,
-14, -7, -20, -10, -5, -14, -7, 20, 10 …
Side note: Sandra Perez of Mesa College, San Diego, presented this paper at the MCRC in 2019:
Update (6/8/2020):
As a challenge listed in Project Euler (see other post), I wrote a Python program to calculate long Collatz chains. For starting numbers under 10,000,000, the number 8,400,511 produces the longest chain at 685 entries which I list below beginning with the entry after the start number: [25201534, 12600767, 37802302, 18901151, 56703454, 28351727, 85055182, 42527591, 127582774, 63791387, 191374162, 95687081, 287061244, 143530622, 71765311, 215295934, 107647967, 322943902, 161471951, 484415854, 242207927, 726623782, 363311891, 1089935674, 544967837, 1634903512, 817451756, 408725878, 204362939, 613088818, 306544409, 919633228, 459816614, 229908307, 689724922, 344862461, 1034587384, 517293692, 258646846, 129323423, 387970270, 193985135, 581955406, 290977703, 872933110, 436466555, 1309399666, 654699833, 1964099500, 982049750, 491024875, 1473074626, 736537313, 2209611940, 1104805970, 552402985, 1657208956, 828604478, 414302239, 1242906718, 621453359, 1864360078, 932180039, 2796540118, 1398270059, 4194810178, 2097405089, 6292215268, 3146107634, 1573053817, 4719161452, 2359580726, 1179790363, 3539371090, 1769685545, 5309056636, 2654528318, 1327264159, 3981792478, 1990896239, 5972688718, 2986344359, 8959033078, 4479516539, 13438549618, 6719274809, 20157824428, 10078912214, 5039456107, 15118368322, 7559184161, 22677552484, 11338776242, 5669388121, 17008164364, 8504082182, 4252041091, 12756123274, 6378061637, 19134184912, 9567092456, 4783546228, 2391773114, 1195886557, 3587659672, 1793829836, 896914918, 448457459, 1345372378, 672686189, 2018058568, 1009029284, 504514642, 252257321, 756771964, 378385982, 189192991, 567578974, 283789487, 851368462, 425684231, 1277052694, 638526347, 1915579042, 957789521, 2873368564, 1436684282, 718342141, 2155026424, 1077513212, 538756606, 269378303, 808134910, 404067455, 1212202366, 606101183, 1818303550, 909151775, 2727455326, 1363727663, 4091182990, 2045591495, 6136774486, 3068387243, 9205161730, 4602580865, 13807742596, 6903871298, 3451935649, 10355806948, 5177903474, 2588951737, 7766855212, 3883427606, 1941713803, 5825141410, 2912570705, 8737712116, 4368856058, 2184428029, 6553284088, 3276642044, 1638321022, 819160511, 2457481534, 1228740767, 3686222302, 1843111151, 5529333454, 2764666727, 8294000182, 4147000091, 12441000274, 6220500137, 18661500412, 9330750206, 4665375103, 13996125310, 6998062655, 20994187966, 10497093983, 31491281950, 15745640975, 47236922926, 23618461463, 70855384390, 35427692195, 106283076586, 53141538293, 159424614880, 79712307440, 39856153720, 19928076860, 9964038430, 4982019215, 14946057646, 7473028823, 22419086470, 11209543235, 33628629706, 16814314853, 50442944560, 25221472280, 12610736140, 6305368070, 3152684035, 9458052106, 4729026053, 14187078160, 7093539080, 3546769540, 1773384770, 886692385, 2660077156, 1330038578, 665019289, 1995057868, 997528934, 498764467, 1496293402, 748146701, 2244440104, 1122220052, 561110026, 280555013, 841665040, 420832520, 210416260, 105208130, 52604065, 157812196, 78906098, 39453049, 118359148, 59179574, 29589787, 88769362, 44384681, 133154044, 66577022, 33288511, 99865534, 49932767, 149798302, 74899151, 224697454, 112348727, 337046182, 168523091, 505569274, 252784637, 758353912, 379176956, 189588478, 94794239, 284382718, 142191359, 426574078, 213287039, 639861118, 319930559, 959791678, 479895839, 1439687518, 719843759, 2159531278, 1079765639, 3239296918, 1619648459, 4858945378, 2429472689, 7288418068, 3644209034, 1822104517, 5466313552, 2733156776, 1366578388, 683289194, 341644597, 1024933792, 512466896, 256233448, 128116724, 64058362, 32029181, 96087544, 48043772, 24021886, 12010943, 36032830, 18016415, 54049246, 27024623, 81073870, 40536935, 121610806, 60805403, 182416210, 91208105, 273624316, 136812158, 68406079, 205218238, 102609119, 307827358, 153913679, 461741038, 230870519, 692611558, 346305779, 1038917338, 519458669, 1558376008, 779188004, 389594002, 194797001, 584391004, 292195502, 146097751, 438293254, 219146627, 657439882, 328719941, 986159824, 493079912, 246539956, 123269978, 61634989, 184904968, 92452484, 46226242, 23113121, 69339364, 34669682, 17334841, 52004524, 26002262, 13001131, 39003394, 19501697, 58505092, 29252546, 14626273, 43878820, 21939410, 10969705, 32909116, 16454558, 8227279, 24681838, 12340919, 37022758, 18511379, 55534138, 27767069, 83301208, 41650604, 20825302, 10412651, 31237954, 15618977, 46856932, 23428466, 11714233, 35142700, 17571350, 8785675, 26357026, 13178513, 39535540, 19767770, 9883885, 29651656, 14825828, 7412914, 3706457, 11119372, 5559686, 2779843, 8339530, 4169765, 12509296, 6254648, 3127324, 1563662, 781831, 2345494, 1172747, 3518242, 1759121, 5277364, 2638682, 1319341, 3958024, 1979012, 989506, 494753, 1484260, 742130, 371065, 1113196, 556598, 278299, 834898, 417449, 1252348, 626174, 313087, 939262, 469631, 1408894, 704447, 2113342, 1056671, 3170014, 1585007, 4755022, 2377511, 7132534, 3566267, 10698802, 5349401, 16048204, 8024102, 4012051, 12036154, 6018077, 18054232, 9027116, 4513558, 2256779, 6770338, 3385169, 10155508, 5077754, 2538877, 7616632, 3808316, 1904158, 952079, 2856238, 1428119, 4284358, 2142179, 6426538, 3213269, 9639808, 4819904, 2409952, 1204976, 602488, 301244, 150622, 75311, 225934, 112967, 338902, 169451, 508354, 254177, 762532, 381266, 190633, 571900, 285950, 142975, 428926, 214463, 643390, 321695, 965086, 482543, 1447630, 723815, 2171446, 1085723, 3257170, 1628585, 4885756, 2442878, 1221439, 3664318, 1832159, 5496478, 2748239, 8244718, 4122359, 12367078, 6183539, 18550618, 9275309, 27825928, 13912964, 6956482, 3478241, 10434724, 5217362, 2608681, 7826044, 3913022, 1956511, 5869534, 2934767, 8804302, 4402151, 13206454, 6603227, 19809682, 9904841, 29714524, 14857262, 7428631, 22285894, 11142947, 33428842, 16714421, 50143264, 25071632, 12535816, 6267908, 3133954, 1566977, 4700932, 2350466, 1175233, 3525700, 1762850, 881425, 2644276, 1322138, 661069, 1983208, 991604, 495802, 247901, 743704, 371852, 185926, 92963, 278890, 139445, 418336, 209168, 104584, 52292, 26146, 13073, 39220, 19610, 9805, 29416, 14708, 7354, 3677, 11032, 5516, 2758, 1379, 4138, 2069, 6208, 3104, 1552, 776, 388, 194, 97, 292, 146, 73, 220, 110, 55, 166, 83, 250, 125, 376, 188, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
 Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
 Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
 Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
 Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
 Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.
Adjunct faculty member of the University of Redlands, School of Business.
Retired Quality Engineering Manager - Abbott Labs (32 years).
Favorite classes to teach: Management Science, Statistics, Operations Management, Analytics.
Contributor to the Online Encyclopedia of Integer Sequences (OEIS) https://oeis.org/.


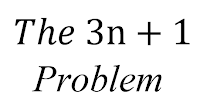



.png)