Atomic interstitial sizes in higher dimensions

As a student years ago in Materials Science and Engineering, I learned how to calculate the size of the largest interstitial atom that could fit within the various cubic and close packed structures of metals. This is important for understanding alloy design and hardening mechanisms in metals. An interstitial atom is one that fits between the gaps of the host atoms. This is in contrast to a substitutional atom which simply replaces one of the host atoms in the atomic arrangement. A substitutional atom typically has a size very similar to the host atom. In the case of an interstitial atom, it is usually much smaller as it has to fit within the gaps of the host structure. However, is this always the case?

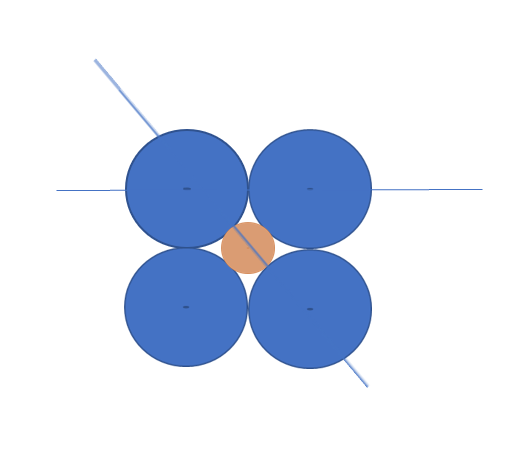
The simplest example starts with a two-dimensional array of atoms in a cubic structure.  

If one is trying to determine the diameter of the largest possible interstitial atom, consider the tan colored atom in the middle of the four blue host atoms. We calculate the length of the diagonal line from the center of one blue atom, through the tan atom, and to the center of the other blue atom. The length of this line is D + d, where D is the diameter of the blue atoms and d is the diameter of the interstitial. In this cubic arrangement, the length of this line can also be calculated from the Pythagorean Theorem and is the square-root of (D² + D²). Setting the two forms of the length of the diagonal to be:

Numerically, d is approximately 0.414 D,

Next, consider the three-dimensional arrangement of atoms in a simple cubic arrangement. The same type of calculation can be made but with a great diagonal running from one corner atom to the opposite corner.

Again, the length of the diagonal is D + d. The Pythagorean Theorem can also be applied in three dimensions and so the diagonal also equals the square-root of (D² + D² + D²). Setting the two terms for the diagonal to be equal gives the largest d, that can fit within the atoms of diameter D:

Numerically, this is approximately 0.732 D. This is known as Kepler's conjecture - described in the book: Math Vacation: Book Review – Instant Mathematics by Paul Parsons and Gail Dixon (jamesmacmath.blogspot.com).

While we don't have examples of four-dimensional arrangements of atoms, something interesting happens. The size of the largest interstitial atom that can fit within the host atoms is the same size of the host atom.

Following the examples for the two- and three-dimensional interstitial atoms, the size d is:

There is no reason to stop there. In five dimensions, the size of the interstitial space is larger than the host atom itself:

Update 9/25/2022: The Ukranian mathematician, Maryna Sergiivna Viazovska (Марина Сергіївна Вязовська), won the Fields Medal this year on sphere packing in higher dimensions.