Atomic interstitial sizes in higher dimensions

As a student years ago in Materials Science and Engineering, I learned how to calculate the size of the largest interstitial atom that could fit within the various cubic and close packed structures of metals. This is important for understanding alloy design and hardening mechanisms in metals. An interstitial atom is one that fits between the gaps of the host atoms. This is in contrast to a substitutional atom which simply replaces one of the host atoms in the atomic arrangement. A substitutional atom typically has a size very similar to the host atom. In the case of an interstitial atom, it is usually much smaller as it has to fit within the gaps of the host structure. However, is this always the case?

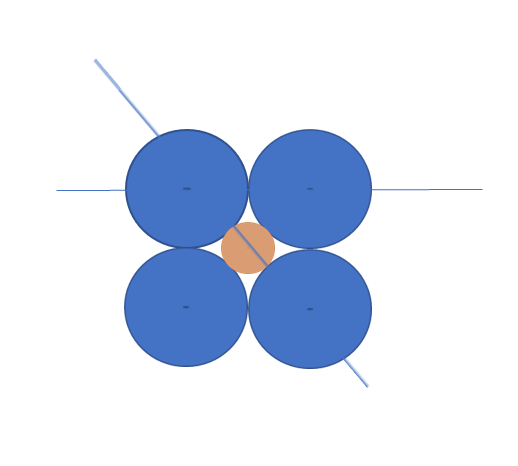
The simplest example starts with a two-dimensional array of atoms in a cubic structure.  

If one is trying to determine the diameter of the largest possible interstitial atom, consider the tan colored atom in the middle of the four blue host atoms. We calculate the length of the diagonal line from the center of one blue atom, through the tan atom, and to the center of the other blue atom. The length of this line is D + d, where D is the diameter of the blue atoms and d is the diameter of the interstitial. In this cubic arrangement, the length of this line can also be calculated from the Pythagorean Theorem and is the square-root of (D² + D²). Setting the two forms of the length of the diagonal to be:

Numerically, d is approximately 0.414 D,

Next, consider the three-dimensional arrangement of atoms in a simple cubic arrangement. The same type of calculation can be made but with a great diagonal running from one corner atom to the opposite corner.

Again, the length of the diagonal is D + d. The Pythagorean Theorem can also be applied in three dimensions and so the diagonal also equals the square-root of (D² + D² + D²). Setting the two terms for the diagonal to be equal gives the largest d, that can fit within the atoms of diameter D:

Numerically, this is approximately 0.732 D. This is known as Kepler's conjecture - described in the book: Math Vacation: Book Review – Instant Mathematics by Paul Parsons and Gail Dixon (jamesmacmath.blogspot.com).

While we don't have examples of four-dimensional arrangements of atoms, something interesting happens. The size of the largest interstitial atom that can fit within the host atoms is the same size of the host atom.

Following the examples for the two- and three-dimensional interstitial atoms, the size d is:

There is no reason to stop there. In five dimensions, the size of the interstitial space is larger than the host atom itself:

Update 9/25/2022: The Ukranian mathematician, Maryna Sergiivna Viazovska (Марина Сергіївна Вязовська), won the Fields Medal this year on sphere packing in higher dimensions.

Book Review: It's a Numberful World: How Math Is Hiding Everywhere

 

I was recently asked why I read so many books about math. People say "haven't you already learned those concepts" or "what are you finding that is new." I keep reading more math books by different authors because I do find new ideas. Sure, it may be some concept that was taught to me years ago or that I read by another author, but I continue to learn from others who explain concepts a little differently than other teachers and authors. As a part-time educator, I'm appreciate new or different ways to explain mathematical concepts to students. 

Eddie Woo's book is packed with 26 bite-size chapters explaining concepts from number theory, knot theory, magic tricks, ciphers, mathematical proofs, and more. Each chapter has practical applications, explanations, and refreshingly good graphics (compliments to Alissa Dinallo). I highly recommend this book for parents or teachers of middle-school to high-school students and to others, like me, looking for a good read.

Eddie Woo's website is: Wootube – Find joy in learning mathematics. (misterwootube.com)

His book site is: Books + TV – Wootube (misterwootube.com)

Abraham Lincoln - A President Trained by Euclid

In studying law, Abraham Lincoln (16th United States of America President) came across the word demonstrate frequently. He searched for further meaning. Consulting Websters, he found “certain proof” and “proof beyond the possibility of doubt.” 

So, what did Lincoln do? He studied the works of Euclid – six volumes of geometric proofs and he mastered all of them. Proofs where a proposition is demonstrated beyond doubt based on a foundation of facts and logic. We don’t know Lincoln as a mathematician, but we do know him as a famous debater and orator.

Geometry in high school is the point at which students either really start to understand the mathematical process or really despise math.

It’s in geometry where we learn how to set-up a proof. We start with given axioms and step, by step, we establish a proof. At the end of the proof, it is the practice to write “Q.E.D.” Which is the Latin acronym for Q.E.D., Quod erat demonstrandum -

– That which is to be demonstrated.

 Some of this chain of logic is seen in the 1^st paragraph of the Gettysburg Address (note the term proposition):

             "Four score and seven years ago our fathers brought forth upon this continent, a new nation, conceived in Liberty, and dedicated to the proposition that all men are created equal."

Another example is from AL’s private notes in 1854 (perhaps formulating an opposing viewpoint to those who tried to justify slavery):

“If A can prove, however conclusively, that he may, of right, enslave B – why may not B snatch the same argument, and prove equally, that he may enslave A.” Source: Abraham Lincoln: A Life by Michael Burlingame, Johns Hopkins University Press, 2013.

Also, in the ending paragraph of AL 1^st inaugural address (more of a music analogy but linked by chords and harmony to math):

The mystic chords which, proceeding from so many battlefields and so many patriot graves, pass through all the hearts and all hearths in this broad continent of ours, will yet again harmonize in their ancient music when breathed upon by the guardian angel of the nation.

So, Lincoln learned from the discipline of geometry how to make a solid, logical argument and how make a proof.

1.   Carpenter, F.B. The Inner Life of Abraham Lincoln: Six Months at the White House Hurd & Houghton, New York, NY (1874).

Article: From Euclid to Abraham Lincoln, Logical Minds Think Alike (nautil.us)